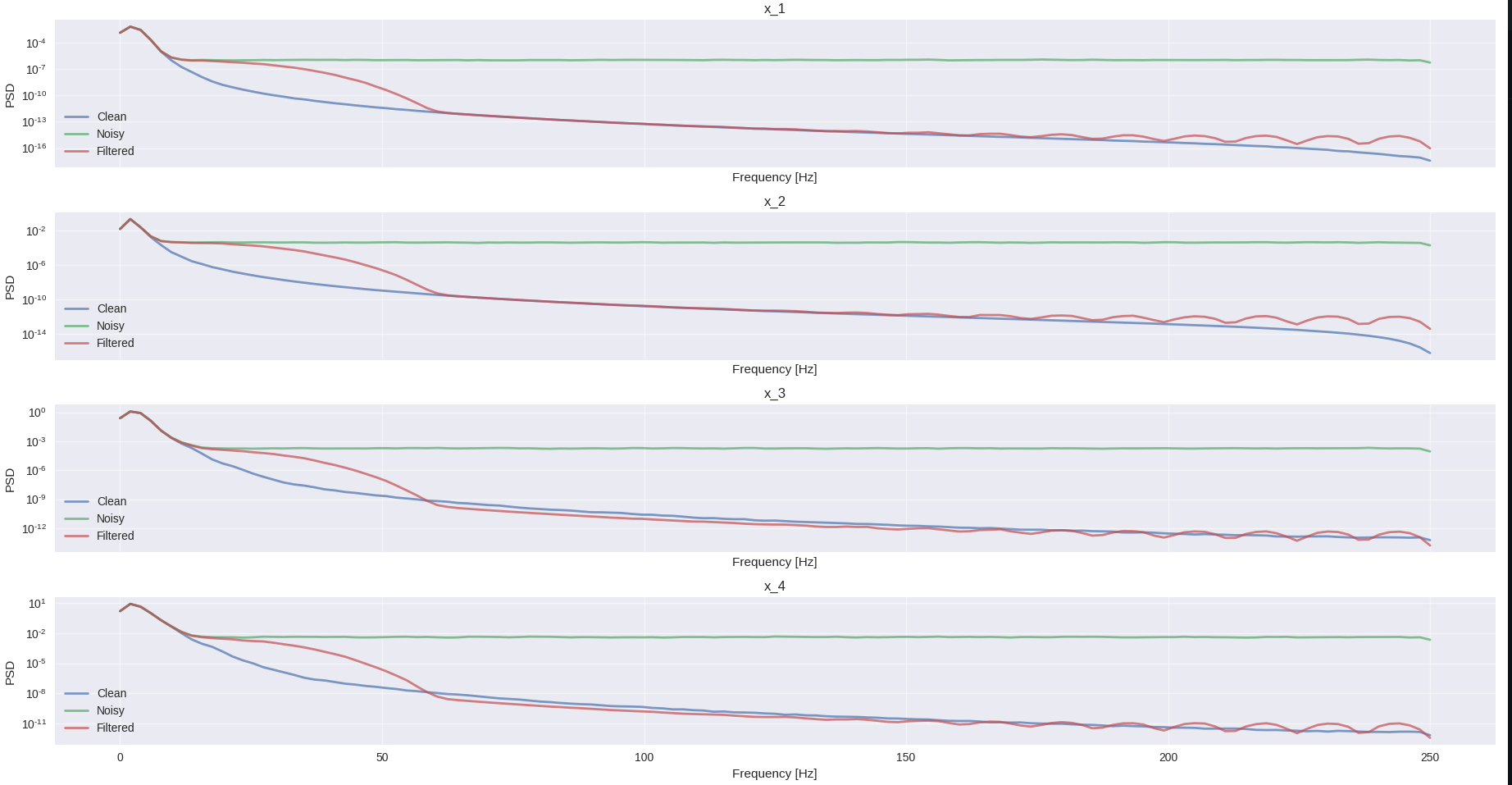
Discovering the governing equations of nonlinear systems purely from data using the SINDy method (https://www.pnas.org/content/113/15/3932).
Lorenz system simulation with feedforward strongly nonlinear inputs. This simulation data was used for identification. https://user-images.githubusercontent.com/55796835/127328774-a1342b36-4729-4225-8e3e-fd447fc66a5e.mp4
Lorenz system simulation with feedback inputs. Used for demonstration of identification of a controlled system. Note that the state gravitates more strongly to the right attractor, where it's being pushed by the control law. https://user-images.githubusercontent.com/55796835/127328914-39fbc4ed-b294-48a5-9ac7-729e497d5644.mp4
Simulation of the reference Lorenz model and the model identified from its measurement data. https://user-images.githubusercontent.com/55796835/127679128-65357765-4e09-4b51-9d53-e436224f4084.mp4
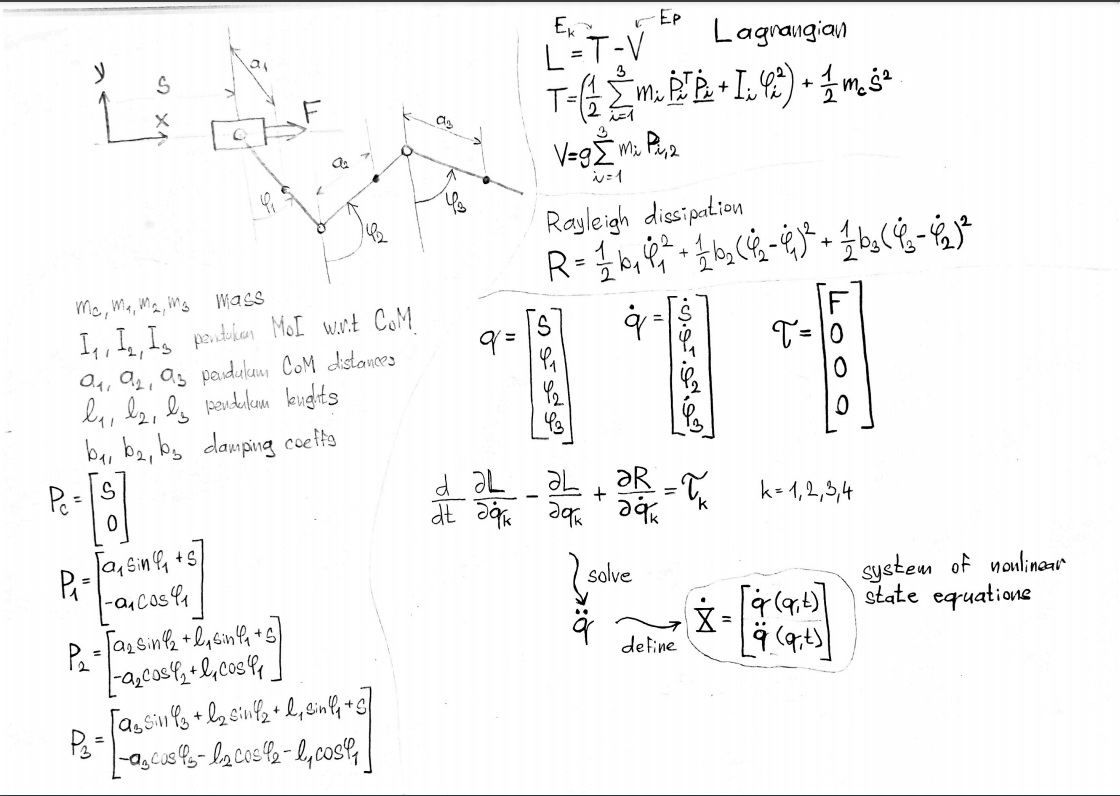
Simulation of the pendulum-cart system https://user-images.githubusercontent.com/55796835/127646378-228cc491-b344-4ab0-9caf-d83239d9fb81.mp4
Simulation of the reference pendulum-cart model and model identified using SINDy from noisy data. https://user-images.githubusercontent.com/55796835/127749887-452fa243-7efa-4761-86bd-0d9dca009ddb.mp4
Reference model vs Bootstrapped model https://user-images.githubusercontent.com/55796835/127749898-489bcebc-fb2e-4f7f-bea3-ada7994ee317.mp4
SINDy model vs Bootstrapped model https://user-images.githubusercontent.com/55796835/127749894-e9e21523-7ae3-4ad0-b916-287db34bbfc4.mp4
Lorenz reference vs identified, nonlinear and discontinuous input sgn(u1) to dx1 https://user-images.githubusercontent.com/55796835/127779031-6db32467-f23b-4574-8389-3a0982e1bd85.mp4
Model identified from real measurement data https://user-images.githubusercontent.com/55796835/127922658-35e7b487-f04e-431a-a6e0-aed10cce4e76.mp4
The real measurement data, visualized https://user-images.githubusercontent.com/55796835/127937959-67bdb377-eedd-4c89-b2cd-edfd253517ce.mp4