Respect the chunksize in forward-mode AD about sparsedifftools.jl HOT 5 CLOSED

https://github.com/FluxML/Zygote.jl/blob/ce8111da692f776f7a8973cf32497319252a0559/src/lib/forward.jl#L12-L34 shows how to do it.

from sparsedifftools.jl.

Yes, the idea is that p should turn into an array of arrays for the partials, and you iterate through running f on p[i].

Now we can pass this vector of partials to the function, iterate over it in the function body, for each partial_i in partials_array, compute the partial Jacobian, and save it in J. We don't decompress it yet. Instead, as we move to the next value of partial_i and compute more values of the Jacobian, we add them to the previously computed J itself. There will be no collision due to the way coloring works. Once all the partials have been computed, our compressed Jacobian will consist of all the final values. Now we can use the previously implemented decompression logic to obtain the original Jacobian.

After each call of f you'll want to decompress into the sparse J. The reason for this is because you don't have the dense compressed Jacobian allocated anywhere, and you won't want to allocate the big matrix if you don't have to. f call on p[i], decompress into the true J, then to it with the next p, the next p, etc. It's a lot like the numerical differentiation form actually.

from sparsedifftools.jl.

No, you're chunking the wrong way. If you take a chunk size 2, then you'd have 2 partials at max, so you'd do:

1 0
0 1
0 0
1 0
0 1
0 0
1 0
0 1
0 0

and then the next chunk would solve with just one partial, but you might pad it just for type-stability (or Val(maximum(colors)) the dispatch to generate more precise code, but those are details).

The reason is because if you have 3000 colors, you don't want to solve with a 3001 dimensional number since you'd run out of memory, so you use 16 dimensional numbers and patch it back together.

Decompressing is then the same as the full case, since that was done by partial, and now you just compute the partials in chunks.

from sparsedifftools.jl.

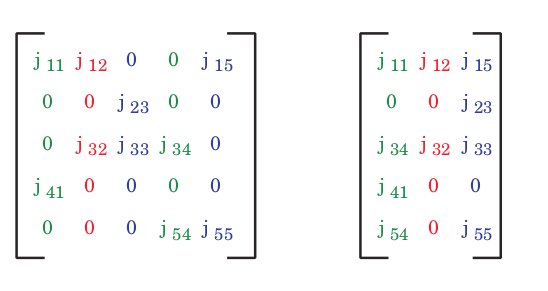
Consider this Jacobian matrix :

This will give us the coloring vector: [1,2,3,1,3]
which in turn will give us the seed matrix (from which we derive the partials):

[[1, 0, 0],
 [0 ,1 ,0],
 [0, 0, 1],
 [1, 0, 0],
 [0, 0, 1]]

Now say if the chunksize is set to 3, then we are supposed to pass only 3 partials for the first AD call, so the partials that we'll be passing would look something like:

[[1, 0, 0],
 [0 ,1 ,0],
 [0, 0, 1],
 [0, 0, 0],
 [0, 0, 0]]

My idea is, instead of immediately passing these partials to the forwarddiff_color_jacobian!, can we store them in an array, say partials_array, whose first element will be the above shown partials list (converted to a tuple perhaps), and second element would look like:

[[0, 0, 0],
 [0 ,0 ,0],
 [0, 0, 0],
 [1, 0, 0],
 [0, 0, 1]]

Now we can pass this vector of partials to the function, iterate over it in the function body, for each partial_i in partials_array, compute the partial Jacobian, and save it in J. We don't decompress it yet. Instead, as we move to the next value of partial_i and compute more values of the Jacobian, we add them to the previously computed J itself. There will be no collision due to the way coloring works. Once all the partials have been computed, our compressed Jacobian will consist of all the final values. Now we can use the previously implemented decompression logic to obtain the original Jacobian.

Can you tell me if you see any flaws or problems with the logic or the implementation anywhere? I think you probably wanted me to decompress the column elements into their actual positions with each partial computation, but I believe this method would be much easier to implement without any obvious drawbacks or performance loss. Thoughts?

from sparsedifftools.jl.

The complete partial (and the seed matrix) for a tridiagonal matrix looks like:

1 0 0
0 1 0
0 0 1
1 0 0
0 1 0
0 0 1
1 0 0
0 1 0
0 0 1

Now if we take the chunk size as 3, then for the first pass, the dual number will have a partial that will look like:

1 0 0
0 1 0
0 0 1
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0

which in turn gives us the partially-computed columns of the Jacobians:

-2 1 0
1 -2 1
0 1 -2
0 0 1
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0

Here, if we consider the column colored with color 1, which is dx = [-2 1 0 0 0 0 0 0 0]', how are we supposed to determine if the 0 at the third index is the value of the derivative or a zero due to the sparsity pattern?
It might be possible that the element at J[3,4] could be a 0, which would result in the exact same dx, and would satisy the coloring condition as well as the non-zero condition at position [3,4] in the sparsity pattern.

from sparsedifftools.jl.